Demystifying Boolean Logic: A Comprehensive Guide To Karnaugh Maps

Demystifying Boolean Logic: A Comprehensive Guide to Karnaugh Maps

Related Articles: Demystifying Boolean Logic: A Comprehensive Guide to Karnaugh Maps

Introduction

With enthusiasm, let’s navigate through the intriguing topic related to Demystifying Boolean Logic: A Comprehensive Guide to Karnaugh Maps. Let’s weave interesting information and offer fresh perspectives to the readers.

Demystifying Boolean Logic: A Comprehensive Guide to Karnaugh Maps

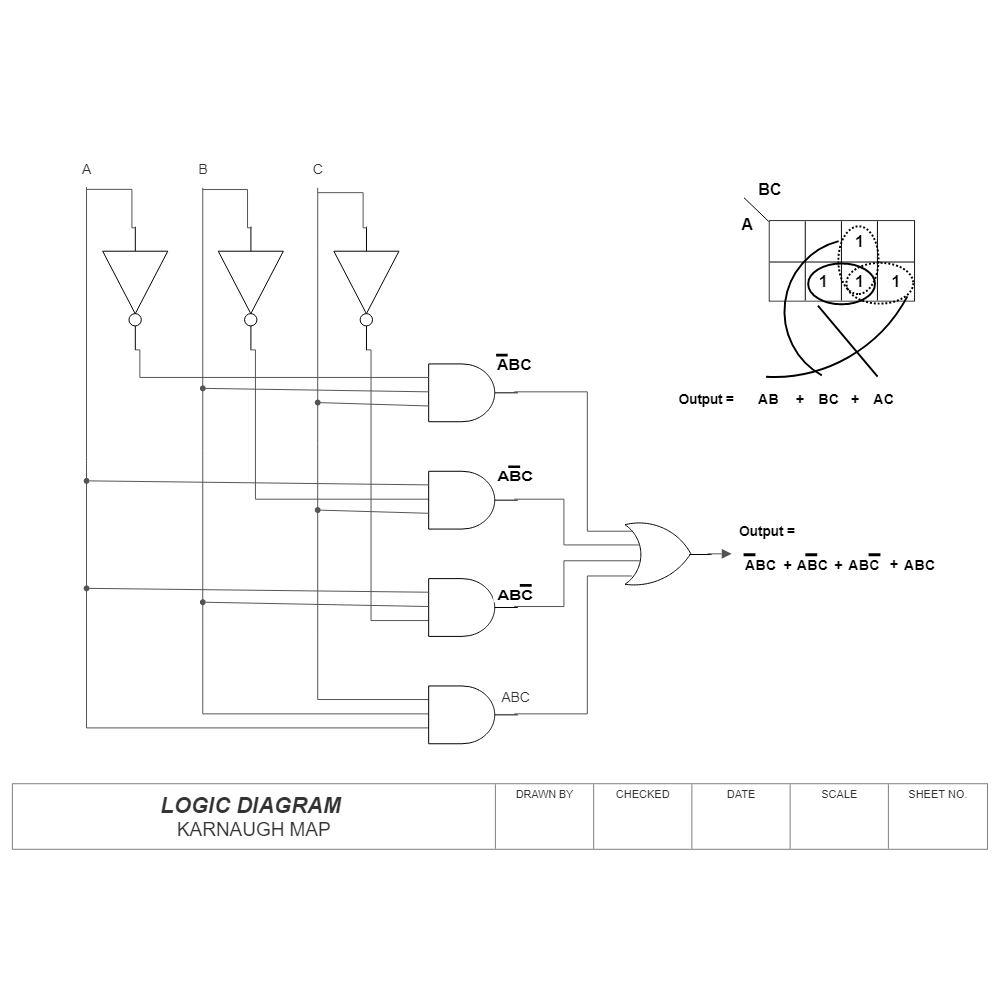
In the realm of digital electronics and computer science, Boolean logic serves as the foundation for designing and analyzing circuits. This system, built upon the fundamental concepts of truth and falsehood, utilizes logical operators like AND, OR, and NOT to manipulate binary values. While understanding these operators is crucial, the process of simplifying complex Boolean expressions can be challenging. This is where Karnaugh maps, also known as K-maps, emerge as a powerful tool, offering a visual and intuitive approach to simplification.

Unveiling the Essence of Karnaugh Maps

Karnaugh maps, named after Maurice Karnaugh who introduced them in 1953, are graphical representations of Boolean functions. These maps utilize a grid structure, with each cell representing a unique combination of input variables. The arrangement of these cells follows a specific pattern, ensuring adjacent cells differ by only one variable. This strategic layout facilitates the identification of groups of adjacent "1" cells, representing terms that can be combined to simplify the Boolean expression.

Constructing a Karnaugh Map: A Step-by-Step Guide

The construction of a Karnaugh map involves a series of well-defined steps:

1. Determine the Number of Variables: Begin by identifying the number of input variables in the Boolean function. For instance, a function with three variables would require a 2×4 grid.

2. Assign Binary Values: Label the rows and columns of the map with binary values representing the input variables. The arrangement should follow a Gray code pattern, where adjacent values differ by only one bit.

3. Populate the Map: Evaluate the Boolean function for each possible combination of input variables. Assign a "1" to the corresponding cell if the function evaluates to true (output is 1) and a "0" if it evaluates to false (output is 0).

4. Group the "1" Cells: Identify groups of adjacent "1" cells, including those wrapping around the edges of the map. These groups should be as large as possible and contain a number of cells equal to a power of 2.

5. Write the Simplified Expression: Each group of "1" cells represents a simplified term in the Boolean expression. To derive this term, identify the input variables that remain constant within the group. For instance, a group with a constant value of "1" for the variable ‘A’ and "0" for the variable ‘B’ would result in the term ‘A’ * ‘B’.

Illustrative Example: Simplifying a Boolean Function

Consider the Boolean function:

F(A, B, C) = A’BC + AB’C + ABC + AB’C’

To simplify this function using a Karnaugh map, we follow these steps:

1. Number of Variables: There are three variables (A, B, C).

2. Binary Values: The map will be a 2×4 grid, with rows representing variables A and B, and columns representing variable C.

3. Populate the Map: Evaluate the function for each combination of input variables and populate the map with "1"s and "0"s accordingly:

AB	C’	C
00	0	1
01	0	1
11	1	1
10	0	1

4. Group the "1" Cells: There are two groups of "1" cells:

   • A group of four cells representing the term ‘C’.
   • A group of two cells representing the term ‘AB’.

5. Simplified Expression: The simplified Boolean expression is:

F(A, B, C) = C + AB

This simplified expression is equivalent to the original function but is significantly easier to implement in a digital circuit.

Beyond the Basics: Advanced Applications

Karnaugh maps find wide applications in digital logic design, including:

• Minimizing Logic Circuits: By simplifying Boolean expressions, K-maps reduce the number of logic gates required, leading to smaller, more efficient circuits.
• Identifying Redundant Terms: K-maps can identify redundant terms in Boolean expressions, eliminating unnecessary components from the circuit.
• Implementing Combinational Logic: K-maps provide a visual and intuitive approach to designing and implementing combinational logic circuits, such as adders, decoders, and multiplexers.
• Analyzing Sequential Logic: While primarily used for combinational logic, Karnaugh maps can also be applied to analyze and simplify sequential logic circuits, such as flip-flops and counters.

FAQs on Karnaugh Maps

1. What is the maximum number of variables a Karnaugh map can handle effectively?

The complexity of Karnaugh maps increases with the number of variables. While maps for up to four variables are relatively straightforward, maps for five or more variables become increasingly difficult to manage. For larger numbers of variables, other simplification methods like the Quine-McCluskey algorithm are often preferred.

2. Can Karnaugh maps be used to simplify Boolean expressions with "don’t care" conditions?

Yes, Karnaugh maps can handle "don’t care" conditions, which represent input combinations that are irrelevant to the circuit’s functionality. These conditions can be marked with an "X" on the map and included in groups of "1" cells to further simplify the expression.

3. What are the limitations of Karnaugh maps?

While powerful for simplifying Boolean expressions, Karnaugh maps have limitations:

• Limited to a small number of variables: As mentioned earlier, maps for more than four variables become cumbersome.
• Difficult to visualize for complex expressions: For expressions with many terms or complex logic, the map can become difficult to analyze.
• Not suitable for all Boolean functions: Some functions, especially those with many "don’t care" conditions, may not be effectively simplified using K-maps.

Tips for Using Karnaugh Maps Effectively

• Start with a clear understanding of Boolean logic: A solid grasp of Boolean operators and truth tables is essential for utilizing Karnaugh maps effectively.
• Use a systematic approach: Follow the steps outlined above to construct and analyze the map accurately.
• Identify the largest possible groups: Aim to create groups of "1" cells that are as large as possible, as this leads to the most simplified expression.
• Consider "don’t care" conditions: Utilize "don’t care" conditions strategically to further simplify the expression.
• Practice with various examples: Work through different examples to develop proficiency in using Karnaugh maps.

Conclusion: A Powerful Tool for Simplifying Boolean Logic

Karnaugh maps provide a visual and intuitive approach to simplifying Boolean expressions, making them a valuable tool for digital logic designers. By understanding the principles behind K-maps and applying them effectively, engineers can optimize circuit design, reduce component count, and improve overall system performance. While other simplification methods exist, Karnaugh maps remain a powerful and widely used technique, particularly for smaller-scale Boolean functions. Their ability to simplify complex expressions and identify redundant terms makes them an indispensable tool in the realm of digital logic design.

Closure

Thus, we hope this article has provided valuable insights into Demystifying Boolean Logic: A Comprehensive Guide to Karnaugh Maps. We hope you find this article informative and beneficial. See you in our next article!