Unlocking the Power of Unsupervised Learning: A Comprehensive Guide to Self-Organizing Maps (SOM)
Related Articles: Unlocking the Power of Unsupervised Learning: A Comprehensive Guide to Self-Organizing Maps (SOM)
Introduction
With great pleasure, we will explore the intriguing topic related to Unlocking the Power of Unsupervised Learning: A Comprehensive Guide to Self-Organizing Maps (SOM). Let’s weave interesting information and offer fresh perspectives to the readers.
Table of Content
- 1 Related Articles: Unlocking the Power of Unsupervised Learning: A Comprehensive Guide to Self-Organizing Maps (SOM)
- 2 Introduction
- 3 Unlocking the Power of Unsupervised Learning: A Comprehensive Guide to Self-Organizing Maps (SOM)
- 3.1 Understanding the Essence of Self-Organizing Maps
- 3.2 Key Components of a Self-Organizing Map
- 3.3 The Learning Process: How the SOM Organizes Itself
- 3.4 Unveiling the Power of Self-Organizing Maps: Applications and Benefits
- 3.5 FAQs about Self-Organizing Maps
- 3.6 Tips for Effective SOM Implementation
- 3.7 Conclusion: Embracing the Power of Self-Organization
- 4 Closure
Unlocking the Power of Unsupervised Learning: A Comprehensive Guide to Self-Organizing Maps (SOM)

The realm of machine learning is vast and diverse, encompassing a multitude of techniques designed to extract insights from data. Among these, unsupervised learning stands out as a powerful tool for discovering hidden patterns and structures within data without the need for explicit labels. One prominent unsupervised learning technique, the Self-Organizing Map (SOM), has emerged as a versatile tool with applications spanning various fields.
Understanding the Essence of Self-Organizing Maps
The Self-Organizing Map, also known as the Kohonen map, is a type of artificial neural network that excels at visualizing high-dimensional data in a lower-dimensional space, typically a two-dimensional grid. This process of dimensionality reduction allows for easier comprehension and analysis of complex datasets.
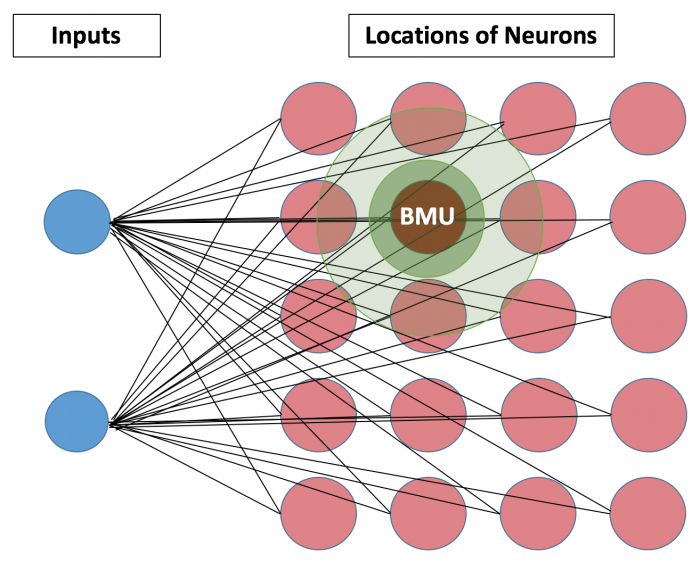
At its core, the SOM operates on the principle of "self-organization," where the network learns to map input data onto a grid of nodes, known as neurons. Each neuron is associated with a weight vector, which represents the neuron’s response to a particular input pattern. During training, the SOM iteratively adjusts the weight vectors of its neurons to minimize the distance between the input data and the corresponding neuron’s representation.
Key Components of a Self-Organizing Map
To understand the inner workings of a SOM, it is crucial to grasp its fundamental components:
- Input Layer: This layer receives the raw data, representing the information to be analyzed.
- Output Layer: This layer consists of a grid of neurons, each with its own weight vector. The neurons are arranged in a two-dimensional space, typically in a rectangular or hexagonal grid.
- Neighborhood Function: This function defines the influence of a neuron on its neighboring neurons during the learning process. The neighborhood function typically decreases with distance, meaning neurons closer to the winning neuron are more strongly influenced.
- Learning Rate: This parameter controls the rate at which the weight vectors are adjusted during training. The learning rate typically decreases over time, ensuring that the network converges to a stable state.
The Learning Process: How the SOM Organizes Itself
The training of a SOM involves a series of iterative steps, where the network gradually learns to map the input data onto its grid of neurons. The process can be summarized as follows:
- Input Presentation: A data point is presented to the input layer.
- Distance Calculation: The input data is compared to the weight vectors of all neurons in the output layer. The neuron with the closest weight vector is declared the "winning neuron."
- Neighborhood Update: The winning neuron and its neighbors have their weight vectors adjusted to become more similar to the input data. The strength of the update depends on the neighborhood function and the learning rate.
- Iteration: Steps 1-3 are repeated for all data points in the training set, multiple times, until the network converges to a stable state.
Unveiling the Power of Self-Organizing Maps: Applications and Benefits
The self-organizing nature of the SOM makes it a powerful tool for various applications, including:
- Data Visualization: SOMs excel at visualizing high-dimensional data in a lower-dimensional space, enabling the identification of clusters and patterns within the data. This is particularly useful in fields like image processing, where complex data can be effectively represented on a 2D map.
- Clustering: SOMs can be used for unsupervised clustering, grouping similar data points together based on their proximity in the output layer. This technique is valuable for market segmentation, customer profiling, and anomaly detection.
- Feature Extraction: By mapping data onto a grid, SOMs can extract relevant features from complex datasets. This information can be used for subsequent classification or prediction tasks.
- Dimensionality Reduction: SOMs effectively reduce the dimensionality of data, simplifying the analysis and making it easier to extract meaningful insights. This is particularly useful when dealing with high-dimensional datasets, such as those encountered in genomics or finance.
- Time Series Analysis: SOMs can be employed to analyze time series data, identifying patterns and trends over time. This is valuable for forecasting, anomaly detection, and understanding dynamic systems.
FAQs about Self-Organizing Maps
1. What are the advantages of using a Self-Organizing Map?
Self-Organizing Maps offer several advantages:
- Unsupervised Learning: SOMs can learn from unlabeled data, making them suitable for exploring data without prior knowledge of the underlying structure.
- Data Visualization: SOMs provide a visual representation of complex data, facilitating the identification of patterns and relationships.
- Dimensionality Reduction: SOMs effectively reduce the dimensionality of data, making it easier to analyze and understand.
- Clustering and Feature Extraction: SOMs can be used for unsupervised clustering and feature extraction, revealing hidden structures and important features within data.
- Adaptability: SOMs can adapt to changes in the input data, making them suitable for dynamic environments.
2. What are the limitations of Self-Organizing Maps?
While powerful, SOMs also have limitations:
- Sensitivity to Initialization: The initial configuration of the network can influence the final results, requiring careful consideration.
- Choice of Parameters: The performance of a SOM is sensitive to the choice of parameters, such as the neighborhood function and learning rate.
- Interpretation of Results: Interpreting the output of a SOM can be challenging, requiring domain expertise and careful analysis.
- Computational Complexity: Training SOMs can be computationally intensive, especially for large datasets.
3. How do I choose the right neighborhood function for my SOM?
The choice of neighborhood function depends on the specific application and the desired level of smoothing. Common choices include:
- Gaussian function: Provides a smooth and gradual decrease in influence with distance.
- Bubble function: Defines a sharp boundary, influencing only neurons within a specific radius.
- Mexican hat function: Provides a combination of excitation and inhibition, influencing nearby neurons while suppressing more distant ones.
4. How do I determine the optimal size of the SOM grid?
The size of the grid should be chosen based on the complexity of the data and the desired level of detail. A larger grid can capture more fine-grained patterns but may require more computational resources.
5. How do I evaluate the performance of my SOM?
The performance of a SOM can be evaluated using various metrics, such as:
- Quantization Error: Measures the average distance between input data points and their corresponding winning neurons.
- Topographic Error: Measures the degree to which neighboring data points are mapped to neighboring neurons on the grid.
- Silhouette Score: Measures the similarity of data points within a cluster compared to other clusters.
Tips for Effective SOM Implementation
- Data Preprocessing: Ensure that the input data is properly scaled and normalized before training the SOM.
- Parameter Tuning: Experiment with different neighborhood functions, learning rates, and grid sizes to find the optimal configuration for your specific problem.
- Visualization: Visualize the output of the SOM to gain insights into the data structure and patterns.
- Interpretation: Use domain knowledge to interpret the results of the SOM and draw meaningful conclusions.
- Evaluation: Use appropriate metrics to assess the performance of the SOM and compare different configurations.
Conclusion: Embracing the Power of Self-Organization
The Self-Organizing Map, with its ability to uncover hidden patterns and structures within data, stands as a testament to the power of unsupervised learning. Its versatility across various domains, from data visualization and clustering to feature extraction and time series analysis, makes it a valuable tool for researchers, analysts, and practitioners alike.
By understanding the principles of SOMs and implementing them effectively, individuals can unlock the potential of this powerful technique to gain deeper insights from their data and make informed decisions in a world driven by information.







Closure
Thus, we hope this article has provided valuable insights into Unlocking the Power of Unsupervised Learning: A Comprehensive Guide to Self-Organizing Maps (SOM). We hope you find this article informative and beneficial. See you in our next article!